There’s something new cooking in how Lucene scores text. Instead of the traditional “TF*IDF,” Lucene just switched to something called BM25 in trunk. That means a new scoring formula for Solr (Solr 6) and Elasticsearch down the line.
Sounds cool, but what does it all mean? In this article I want to give you an overview of how the switch might be a boon to your Solr and Elasticsearch applications. What was the original TF*IDF? How did it work? What does the new BM25 do better? How do you tune it? Is BM25 right for everything?
BM25 and TF*IDF sit at the core of the ranking function. They comprise what Lucene calls the “field weight”. Field weight measures how much matched text is about a search term.
Classic Lucene Similarity: What is TF*IDF?
TF*IDF is a rough way of approximating how users value the relevance of a text match. The intuition underlying TF*IDF is pretty straight-forward and relies on the two principal factors embedded in the name of the scoring formula that tend to correspond to how human minds tend to evaluate search relevance:
- Term Frequency aka tf: how often does “dog” occur in the article? 3 times? 10 times?
- Inverse Document Frequency aka idf: The document frequency measures how many docs a term appears in. Inverse document frequency (
1/df) then measures how special the term is. Is the term “dog” very rare (occurs in just one doc)? Or relatively common (occurs in nearly all the docs)?
In other words, TF*IDF measures the relative concentration of a term in a given piece of text. If “dog” is common in this article, but relatively rare elsewhere, then the TF*IDF score will be high. This article ought to be thought of as very relevant to the search term “dog.” If “dog” occurs once here, but very prominently in many other docs, its score will be relatively low.
One additional measure is the text’s length. “Dog” occurring twice in a 500 pg book says almost nothing about how much that book is about “dog”. “Dog” occurring twice in a short tweet, however, means that tweet is very much about “dog”! Thus an additional bias is introduced called “fieldNorms.” This contribution gives a significant bias towards matching shorter documents over longer documents. The terms are more “concentrated” in the shorter doc, therefore that shorter doc is much more likely to be about the searched-for term and thus should be scored higher.
Classic Lucene Similarity: Fudging TF*IDF
Through constant experimentation, the field of Information Retrieval (the academic side of search) has realized that raw TF IDF values don’t quite correspond to user intuitions of relevance. If an article mentions “dog” six times is it twice as relevant as an article mentioning “dog” 3 times? Most users say no. Sure the article that mentions “dog” 6 times may be more relevant, but not twice as relevant. Similar considerations come into play for a term’s IDF. A term occurring in 500 docs is not twice as special as a term occurring in 1000.
Instead, TF*IDF is modified so that TF, IDF, and field length aren’t taken directly. Instead of TF directly, sqrt(TF) is taken in the scoring formula. Documents with twice the number of terms as another document aren’t twice as relevant. Instead you get a TF score computed as follows
| Raw TF | TF Score |
|---|---|
| 1 | 1.0 |
| 2 | 1.141 |
| 4 | 2.0 |
| 8 | 2.828 |
| 16 | 4.0 |
Ok here with TF, a document with 16 terms is roughly twice as relevant as a document with 4.
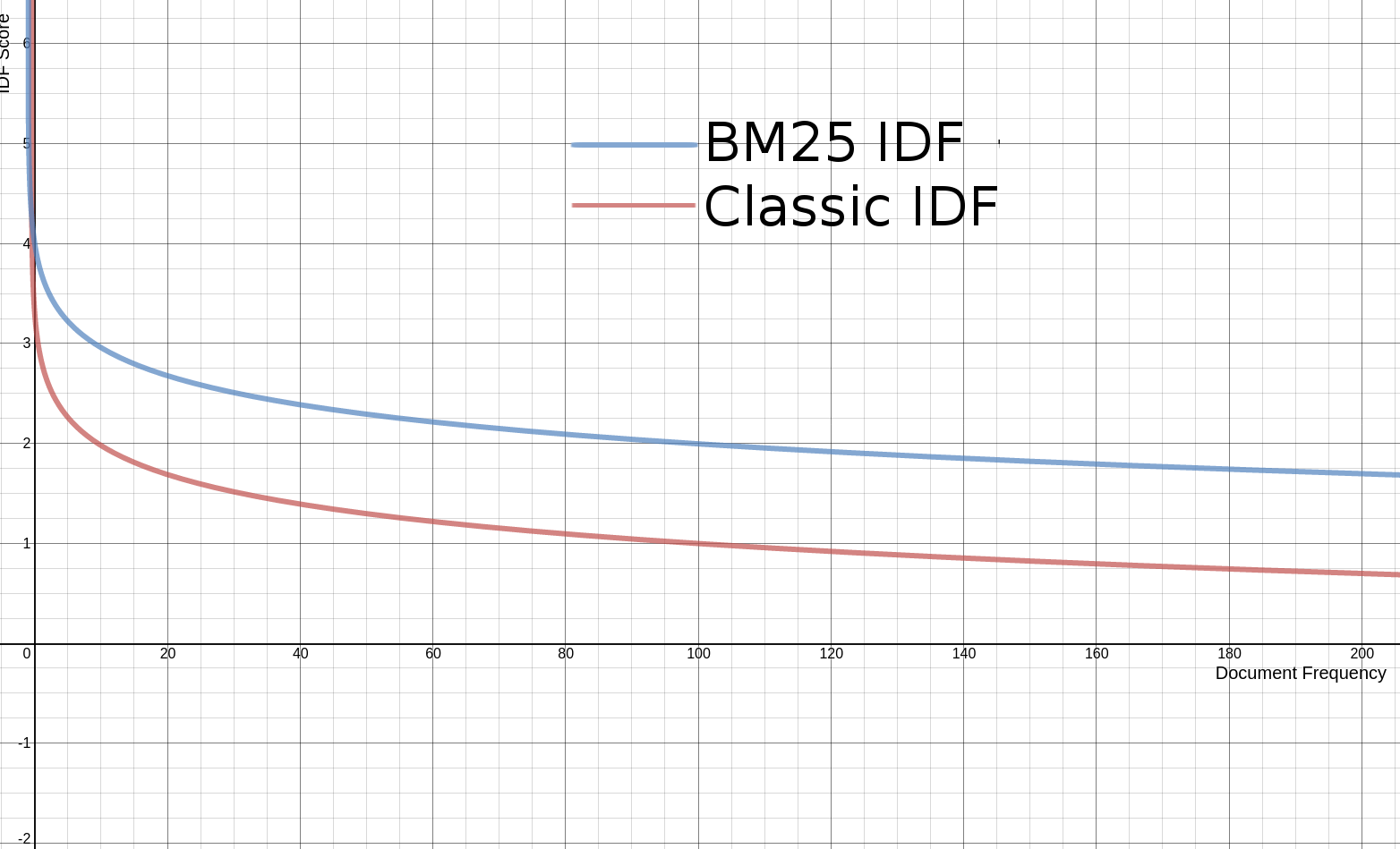
Similarly users don’t consider terms that only occur in 10 documents ten times as special as those that occur in 100 documents. Instead, the IDF score is computed as
log ( numDocs / docFreq + 1) + 1Here numDocs is the number of documents in the corpus. For, say numDocs=1000, this corresponds to::
| Raw DF | IDF Score |
|---|---|
| 1 | 7.214 |
| 2 | 6.809 |
| 4 | 6.298 |
| 64 | 3.733 |
| 128 | 3.048 |
| 256 | 2.359 |
This grows more slowly. Here a term that occurs in only 4 documents is roughly twice as special as a term that occurs in 64 documents. Again, this makes sense intuitively to most users.
What about the impact of a document’s length? How does that computed? This is computed based on another simple formula that also seems to work with user expectations:).
1 / sqrt(length)| Raw Length | Field Norm Score |
|---|---|
| 1 | 1.0 |
| 2 | 0.707 |
| 4 | 0.5 |
| 64 | 0.125 |
| 128 | 0.088 |
| 256 | 0.0625 |
So a length 128 document is roughly ten times less relevant as a match in a length 1 document. This makes a sort of sense based on our intuitions: if you match the only term in a length one document, well that document is absolutely all about that term! In a length 128 document, it’s one of a whole slew of terms and not necessarily what that document is all about.
Classic Lucene Similarity Taken together…
The overall formula is
IDF score * TF score * fieldNormsor
log(numDocs / (docFreq + 1)) * sqrt(tf) * (1/sqrt(length))with the caveats
- numDocs is actually maxDocs, which often counts deleted docs
- fieldNorms are computed and stored as an 8 bit floating point value. Which is terrible precision and creates all kinds of fun problems!
Enter BM25: The Next Generation of TF*IDF
BM25 improves upon TF*IDF. BM25 stands for “Best Match 25”. Released in 1994, it’s the 25th iteration of tweaking the relevance computation. BM25 has its roots in probabilistic information retrieval. Probabilistic information retrieval is a fascinating field unto itself. Basically, it casts relevance as a probability problem. A relevance score, according to probabilistic information retrieval, ought to reflect the probability a user will consider the result relevant. This is a topic that deserves its very own blog post, so I won’t cover it here!
Instead of getting lost in very fascinating theory, I’d rather discuss intuitively how to use BM25. You’ll see the shape the ranking takes, while scary looking mathematically, actually makes a lot of intuitive sense.
BM25’s Take on IDF
Ok first, let’s get IDF out of the way. On a graph, BM25’s IDF looks very similar to classic Lucene IDF. The only reason for the difference here is its derivation from probabilistic information retrieval. Lucene makes one change to BM25’s regular IDF. BM25’s IDF has the potential for giving negative scores for terms with very high document frequency. So IDF in Lucene’s BM25 does this one amazing trick to solve this problem. They add 1 to the value, before taking the log, which makes it impossible to compute a negative value. The end result is an IDF that looks extremely similar to Lucene’s current IDF curve, as shown in the following graph.
So for IDF, not a lot of surprises. We don’t need to alter our thinking about IDF in BM25. What’s more fascinating if you see (again outside the scope of this post) how IDF is derived from probability theory.
BM25’s Take on TF
Now let’s look at term frequency. It’s a bit of a lie to look at term frequency in isolation, but we’re going to try for exposition purposes to build up to the larger BM25 formula.
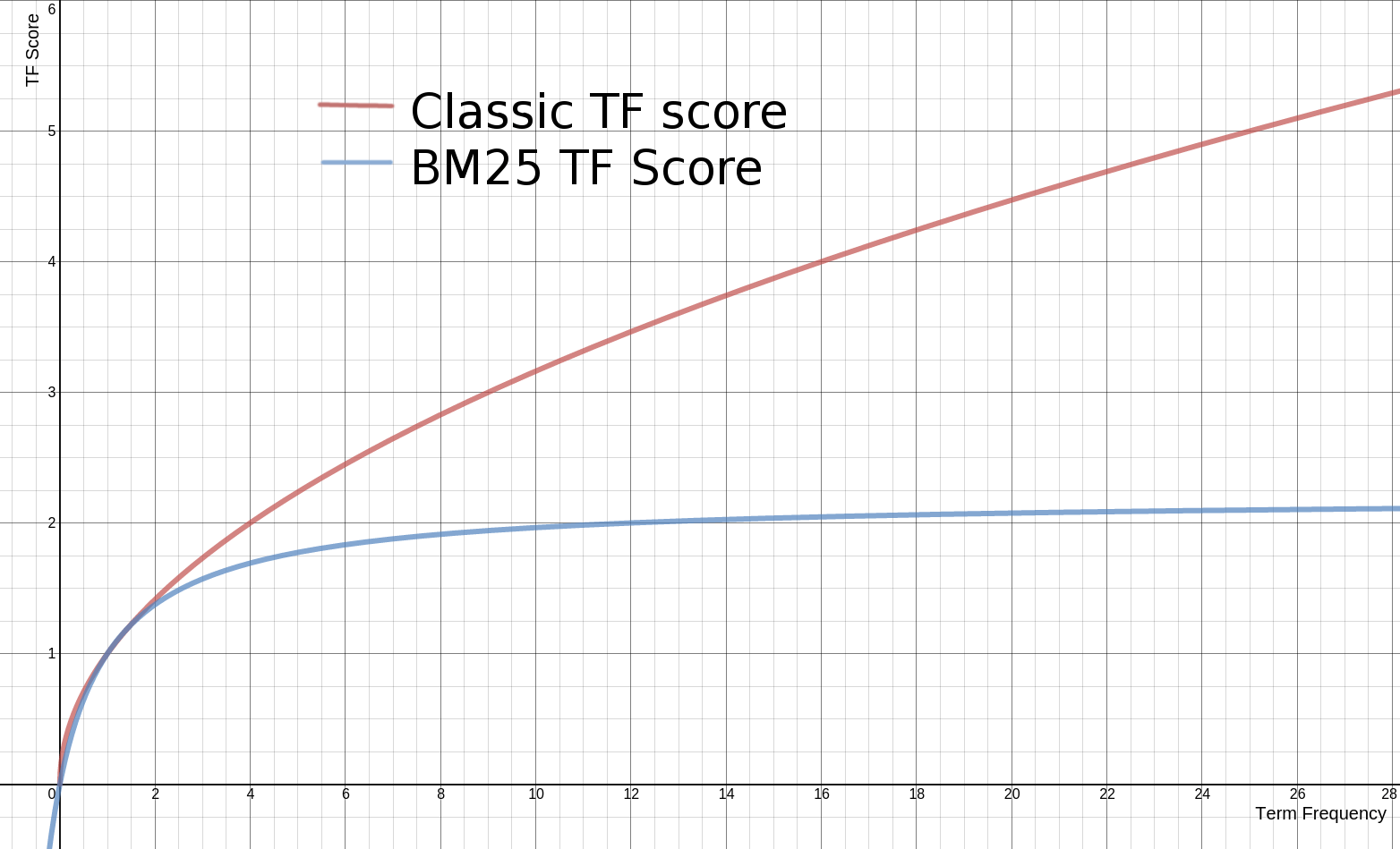
Term frequency in BM25 dampens the impact of term frequency even further than traditional TF*IDF. The impact of term frequency is always increasing, but asymptotically approaches a value.
Without any consideration for document length, term frequency follows the formula
((k + 1) * tf) / (k + tf)as graphed below:
As you can see, this curve approaches (k + 1) asymptotically (here k=1.2). It has a really interesting effect. More tf always means more relevance. However you quickly hit diminishing returns. You never get past k, but you always approach it! Classic Lucene tf, on the other hand, constantly increases and never reaches a saturation point.
What is this k value? For BM25, k is often set to 1.2. Most leave k alone. Changing k though can be a useful tuning approach to modify the impact the TF. Modifying k clearly causes the asymptote to move. However what’s more important is that a higher k causes TF to take longer to reach saturation. By stretching out the point of saturation, you stretch out the relevance difference between higher and lower term frequency docs!
How Does BM25 Use Document Length?
Now the last section was a bit of a useful lie. The TF score above is further influenced by whether the document is above or below the average length of a document in the corpus.
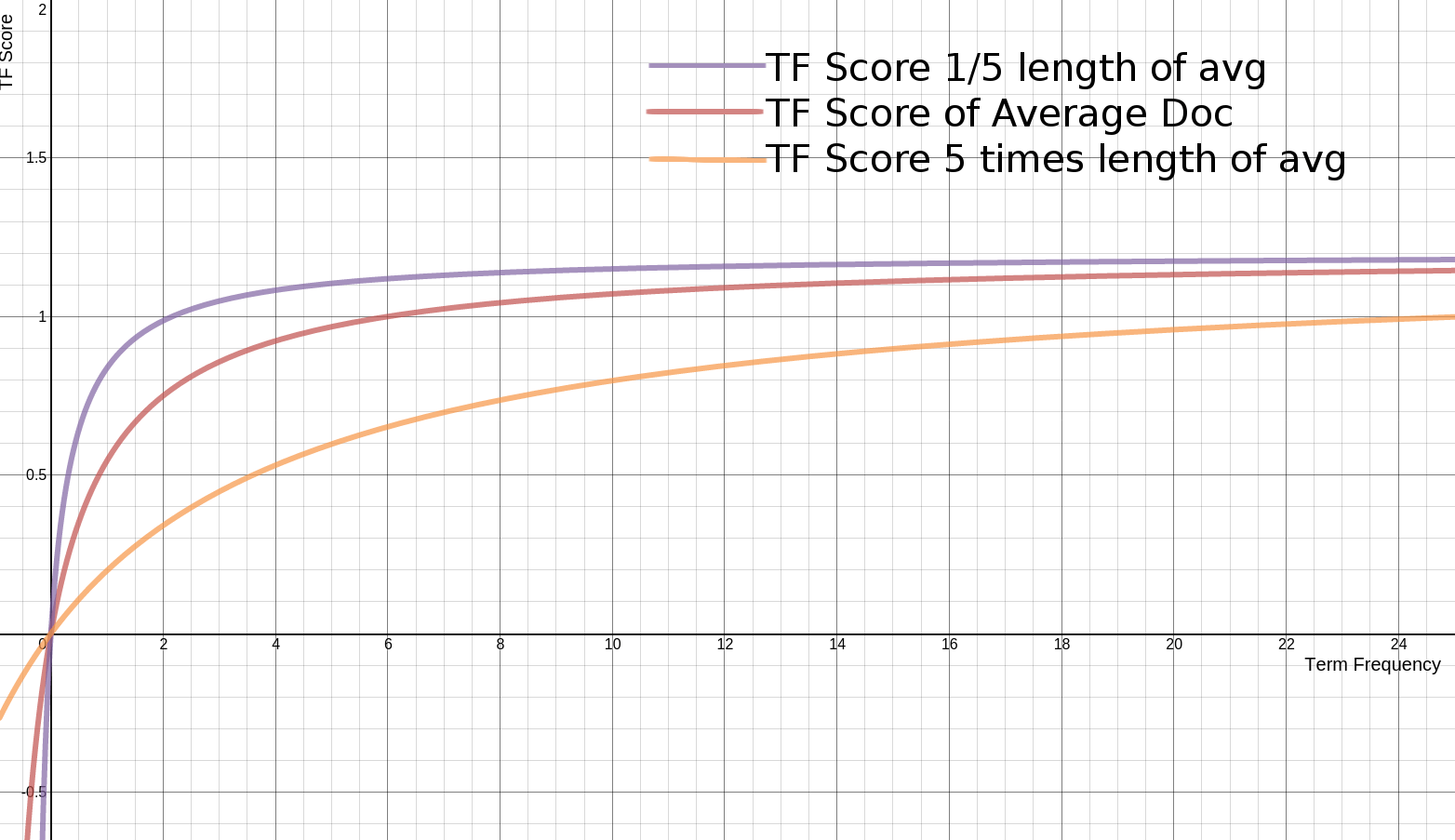
What does this look like? Well let’s built on the TF formula from before, introducing two variables: a constant b and a length value L. Taking the formula above and adding (1.0 - b + b * L) as a multiple on k in the denominator.
((k + 1) * tf) / (k * (1.0 - b + b * L) + tf)Here L is how long a document is relative to the average document length. L is 2 if the document being scored is twice the corpus’s average document length. L is 0.1 if the document being scored is one tenth the average document length. L therefore is actually presented as |d|/avgDl – this document length divided by the average document length.
As you can see in the graph, the end result for different values of L is that shorter docs hit the asymptote much faster. They saturate nearly right away to the best possible TF score. This makes sense, short documents have fewer terms. The more matches in these short docs, the more certain you can feel confident in the relevance. So the number goes up quicker. A lengthy book, on the other hand, takes many more matches to get to a point where we can feel confident. So reaching “max relevance” takes longer.
The constant b will allow us to finely tune how much influence our L value has on scoring. Notice in the formula above, a b of 0 completely removes the influence of L, returning to the formula of the previous section. A higher b adds more document length influence on the scoring. In other words, in classic TF*IDF you always disabled norms on a field to remove the influence of field length. Here you can simply set b to 0 on the similarity to remove the impact of field length.
All Together
When BM25 is taken all together:
IDF * ((k + 1) * tf) / (k * (1.0 - b + b * (|d|/avgDl)) + tf)You can see why we started from square one here!
Will BM25 be appropriate for everything?
I’m really impressed with BM25. I used it on the O’Reilly Library project for searching book chunks. There’s a lot of wisdom here! Term frequency saturation makes a lot of sense. So does modulating the influence of the field length.
But they continue to make sense for article-length pieces of text. Not everything we search are blog posts or wikipedia pages. The similarity being used needs to change based on the kind of thing you are comparing. Title fields, for example have their own wonky proclivities. Indeed hosted search services Algolia and SwiftType make their business in part on being really really good at short snippet search.
So as my buddy Alex from Solr Start asked me – is BM25 right for everyone? For everything? It’s a huge improvement on the core document search problem. But around the edges for numbers, images, and other entities being searched the win is not clear.
This is a fascinating time to be a Lucene, Solr, or Elasticsearch developer. With BM25 becoming the default, we’re going to see directly what happens when theory meets practice. Relevance is never a constant, it’s a user experience you’re crafting. Yet the cauldron that BM25 came out of is information retrieval competitions like Trec and the like. The real world can be so much different. Documents aren’t just documents but restaurants, products, news articles, tweets, doctors’ offices, and many other things. Maybe the right answer for your “similarity” is to always bring up tweets tweeted by friends, nearby with similar interests. Less about text similarity, and more about what’s important for users to find. In other words, search is just as much about crafting a user experience as anything else. That’s why we’re excited about Quepid to help understand the user expectations from search!
Anyway, I’m thoroughly excited about the possibilities of BM25. It opens doors in Lucene’s baseline relevance capabilities and is going to really open a lot of doors for Solr and Elasticsearch capabilities! If you’d like to chat about whether BM25 or another relevance solution is right for your application, please contact us!
Did you know we offer training courses in how to tune relevance for Solr and Elasticsearch based search engines?