The key to really understanding search, recommendations, and other ‘product matching’ systems is microeconomics. Say what!?!? No hear me out. In this article, I want to challenge you to rethink search, recommendations, and other “matching” user experiences through this lens. Thinking in these terms, you’ll see can solve interesting problems of marketplace dynamics that often occur in these domains AND how undervalued these interactions are in maximizing buyer and seller utility.
Microeconomics is defined, according to Wikipedia as:
a branch of economics that studies the behavior of individuals and firms in making decisions regarding the allocation of scarce resources and the interactions among these individuals and firms.
In other words, a marketplace is setup that optimizes the relationships between buyers and sellers. There’s often a market underlying the search, recommendations, advertising, and other bits of ‘discovery’ functionality. Obviously e-commerce is one such domain. But the same factors come into play in job search, dating, real estate to name a few domains.
You be the judge…
One way to test search (we’ll stick to search for now) is to create what’s called a judgment list – a test set for evaluating a given search solution. You can think of a judgment list as a tuple of a grade, search keywords, and the content being searched. This tuple makes a statement that when searching with , should is relevant. Here ranges from 4 (exact match) to 0 (very poor match for a query).
So a common example we might use is a movie search engine. The movie “First Blood” is an exact match for the search keyword Rambo. Whereas “First Daughter” would be an extremely poor match. So we might model such a set of ‘judgments’ as this tab seperated file
grade,keywords,document4
rambo first blood0 rambo first daughterOften identifiers stand in for the actual documents and queries. So in reality, you get something closer to:
4 qid:1 movie1234
0 qid:1 movie5678Of course (and bear with me economists…), there’s more than one use case to consider. In a movie search, we might also have searches for actors. With keywords “Ben Affleck”, for example, we might give a 4 for recent/popular Affleck movies, 3 for older ones, maybe 2 for Affleck movies you’ve never heard of, maybe a 1 for movies with Matt Damon (in case you confuse the two) and 0 for movies not even remotely in the neighborhood of Affleck.
We can add “Ben Affleck” to our judgment list as query id 2:
4 qid:1 movie1234
0 qid:1 movie5678
4 qid:2 movie9499 # The Accountant
4 qid:2 movie5638 # Batman vs Superman
3 qid:2 movie5737 # Good Will Hunting
1 qid:2 movie3727 # Bourne Identity
0 qid:2 movie5678 # First DaughterWe can develop such a judgment list over hundreds, thousands, and more keywords to evaluate the performance of a search system we implement. Common metrics for evaluating indivual searches include NDCG, ERR, or MAP. Each gives each search a score from 0-1 (1 being best). We won’t get into how each of these metrics works, but needless to say each measures different aspects of the search experience.
What does this have to do with microeconomics?
So what does any of this search stuff have to do with economics? One function of an economist is to create models of economic behavior from what we know about buyers, products, situations, etc. Using those models, we hope to create systems (from government policies to organizing store shelves) that help buyers and sellers get what they want and need out of the market.
For example, a shopkeeper has one storefront window to attract buyers. That shopkeeper must balance the diverse needs of potential shoppers. For example, if this is a fitness clothing store: the shopkeeper might wish to attract both the fashionable and practical. To get at both sets of users, the window display shows both the no-frills cheap running clothes right next to the expensive, fashionable yoga pants in the store window.
My storefront window is a limited resource I must use to satisfy the broadest range of reasonable shoppers. I must try to maximize potential buyer’s utility with each displayed item. Utility is a fuzzy economics term, that basically means maximize the chance a desired buyer will find something that satisfies their want or need. And different buyers have competing needs: we might need to sacrifice the percieved utility of one buyer a little to do an even better job attracting other buyers we want to cater towards.
A search engine is just like our storefront window: It’s another system with limited resources (programmer time, maintenance of relevance rules, screen real estate, available features/data, etc) that is attempting to maximize a broad range of competing searcher’s needs. Our judgment list stands in as a proxy for a representative buyer – giving a prioritized preference list for a user with a specific keyword.
Indeed the only difference between a judgment list for search and one for recommendations is whether a query id or a user id is used. A judgment list with a set of users’ ranked preferences, who don’t use keywords, can be used to evaluate recommendation systems. Keeping that in mind, everything we discuss here applies to both search and recommendations even if say “search.”
Using our limited search engine development resources, the closer we get to our users/queries preference list, the higher the chance that user will gain utility from a specific list of search results. Our relevance metrics: NDCG, ERR, etc really stand in for a measurement of this utility.
All of the work we do as relevance engineers, like the classic whack-a-mole game of test driven relevancy, is about trying to maximize the sum of user utility over a group of users. There’s another way to phrase this if you’re mathematically inclined. If user or search queries were on the X axis, and a relevance measure like NDCG the Y axis – our goal is to maximize the integral of NDCG over the users/queries. In other words, trying to maximize the area under this curve:
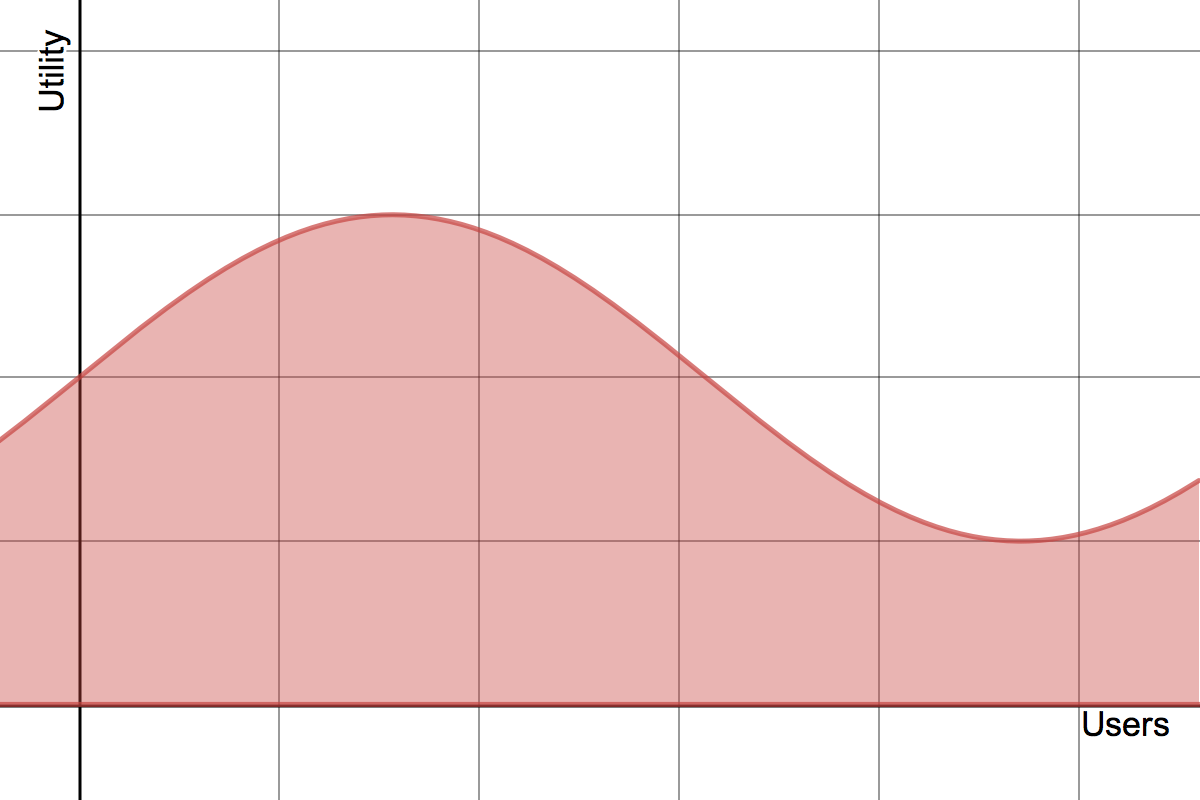
As search/recommendation engineers – what we talk about mundanely as “matching” is really a fundamental activity in the modern market. It might in fact be more accurate to think of ourselves as quantitative traders optimizing short term and long term utility for users as they interact with a brand. Certainly this means showing them the right products and hoping they’ll engage. But one wonders if the entire user experience can be rethought in terms of ‘whats the information (product, info, advice, otherwise) that can be put in front of this user by this brand to maximize the user’s long term utility’ (and as we’ll soon see the utility for the brand).
The Lambda Insight : maximizing competing utilities with machine learning
To see how this can work, let’s get a bit more technical. If you’re familiar with machine learning, judgment lists begin to look like a training set. As a training set, we can use a representative set of judgments and have a machine learning system learn mathematical relationships between the relevance grades and possible features – properties of documents, users, queries, or context. For example, if we have a feature that’s a title relevance score and another that’s time the movie was released into the past, we might have a judgment list cum training set that looks like:
grade, query, doc, timeIntoPast, titleScore, ...
4 qid:1 movie1234 420 0.5 ...
0 qid:1 movie5678 14 5.1
4 qid:2 movie9499 1.5 12
4 qid:2 movie5638 152 5.0
3 qid:2 movie5737 90 2.5
1 qid:2 movie3727 50 11
0 qid:2 movie5678 71 5.9We can treat the grades in such a judgment list as labels in classification or as scalars in a regression. This is precisely what learning to rank attempts to do.
The only oddity compared to other machine learning problems, is that this training set comes grouped by query id. Most machine learning data sets don’t come this way. Predicting a stock market price by profit, number of employees, and other features just has one row per company. Here, we’re not trying to maximize our likelihood of predicting a 0 or a 4 per-se – but instead trying to maximize the likelihood any given user or query will come closest to ranked set of preferences. From our earlier fashion store example how do we balance the needs of the fashionista high-end fashion shopper who wants to drop big cash on yoga pants with the practical cheapskate who wants to just spend $10 without completely disappointing one or the other?
One way to solve this is just to ignore the problem. Some learning to rank approaches as we discussed earlier just directly try to predict the grades. Just chop out the column with qid and perform regression or classification. In other words many approaches go from the judgment list above to:
grade, doc, timeIntoPast, titleScore, ...
4 movie1234 420 0.5 ...
0 movie5678 14 5.1
4 movie9499 1.5 12
4 movie5638 152 5.0
3 movie5737 90 2.5
1 movie3727 50 11
0 movie5678 71 5.9This approach to learning to rank is called point-wise. It’s simple, and it works ok. The problem with point-wise approaches is that by losing the grouping, we’re not really training directly against user utility. During training, a solution that correctly predicts bad search (can successfully give all the 0s 0s) looks just as good as one that always predicts 4s for 4s. We’d clearly rather have the latter. In reality, we’d prefer to be like Santa: doing our best to give every child their first choice. But failing that, maybe we can give some their first choice and others their second. A point-wise approach doesn’t understand that we’re really trying to optimize often competing lists of ranked preferences with a single model.
This is where pair-wise and list-wise learning to rank formulations come in. They flatten the grouped judgment list a bit differently: taking into the account something about how rearranging an item impacts the overall list for a user/keyword. Training so that the NDCG, ERR, or whatever other utility metric is maximized per user directly rather than indirectly through point-wise methods.
One such method is LambdaMART. LambdaMART is a machine learning approach to learning to rank that uses gradient boosted decision trees. But as cool as they sound, gradient boosted decision trees are actually not the most interesting part of LambdaMART. What’s really interesting in LambdaMART is how it solves the flattening problem we just described. In fact, using the LambdaMART creators’ key insight (what I call the lambda insight) could be used to train with any number of machine learning approaches.
But how does the lambda insight work to translate this table
grade, query, doc, timeIntoPast, titleScore, ...
4 qid:1 movie1234 420 0.5 ...
0 qid:1 movie5678 14 5.1
4 qid:2 movie9499 1.5 12
4 qid:2 movie5638 152 5.0
3 qid:2 movie5737 90 2.5
1 qid:2 movie3727 50 11
0 qid:2 movie5678 71 5.9Into “Ys” below that optimize user utility?
grade, doc, timeIntoPast, titleScore, ...
Y movie1234 420 0.5 ...
Y movie5678 14 5.1
Y movie9499 1.5 12
Y movie5638 152 5.0
Y movie5737 90 2.5
Y movie3727 50 11
Y movie5678 71 5.9Lambda ranking works in two stages. I’m going to use the words ‘NDCG’ in the psuedocode below to make it concrete for search folks. In reality though, NDCG can be swapped out for any utility/relevance metric which is one of the amazing things about this algorithm. And this psuedocode is a bit simplified: LambdaMART works iteratively, to constantly improve an existing model. Here though, we just look at the first pass of the algorithm which is the real core of LambdaMART.
# Zero out all the "Ys"For all Judgments A...Z Set A.Y = 0
# Compute new Y's
For each grouped query, sorted in best order:
For each pair of judgments A and B where grade(A) > grade(B)
1. In a temporary list, swap A and B
2. Compute the new, swapped NDCG (which will be a worse NDCG)
3. deltaNDCG = oldNDCG - newNDCG (aka how much worse does this swap make the NDCG score?)
4. A.Y += deltaNDCG
5. B.Y -= deltaNDCGThis algorithm experiments with worsening a user/query’s ranked list of preferences. It computes a delta utility/relevance metric (deltaNDCG) to see how bad it would be to swap these two. Sort of like offering alternate choices to a toddler: “We don’t have string cheese little baby, would you like yogurt instead. Do I get a cute “no” or an emphatic, screeching darth-vader-esque emphatic NOOOOOOOOO!!!!”
Given the magnitude of swapping out my toddler’s favorite food for something else, steps 4 & 5 are where the magic happens. The Ys are updated based on the magnitude of how bad of a swap this would be. The “Ys” here are termed by the author of LambaMART as similar to “forces.” They’re also called “lambdas” (hence the name) or sometimes “psuedo responses”. If swapping A with most other items in this ranked list of preferences, then A.Y will grow quite large. For example if A is string cheese, and toddler really wants string cheese such that no alternative will do, A.Y will go up. I might end up using my limited resources to drive to the store to buy string cheese!
The opposite is also true, if swapping B with most other results makes the results worse, B.Y will be similarly pushed heavily down. Here B might be a food my toddler really dislikes; let’s say tomatoes. It might be worth my limited resources to donate all of our tomatoes, even if it risks arguments with people who sort-of like tomatoes in our home.
Getting this table of “Ys,” let’s one run really any regression solution to try to model the Ys. The creators of LambdaMART try several, eventually settling on gradient boosted decision trees for their use case.
LambdaMART itself though continues working to use psuedo-responses to model the remaining error in the model. This iteratively improves the model. If the existing model is very off kilter and the NDCG deltas are also very high, the next tree will try to compensate for where the other models failed trying to act as a ‘patch’. This basically describes gradient boosting — trying to predict the error of other weak learners by laying on another learner to compensate. I’ll cover gradient boosting in a different article.
What do you want for Christmas?
The combination of maximizing a ranked list, to maximize NDCG is similar to Santa’s job of minimizing disappointment. Ranked lists are great for maximizing utility across a broad set of people. Because if Santa can’t get you your first gift, he can get you number 2. And if giving you your second preference helps Santa give a hundred other kids their first preference: he’s probably going to take that opportunity.
Santa could use the lambda insight to build a model that maximized most children’s satisfaction with their christmas presents based on Santa’s limited resources. Santa can do his best to get closest to everyone’s wishlist. If Santa was using a point-wise model, he’d not take into account the ranked preferences: randomly give some children their 3rd choice, possibly completely missing the first preferences, and not getting nearly as close to optimizing utility across all the children.
I suppose if Santa did use the the lambda insight, he’d be operating philosophically under utilitarianism. But mapping economic philosophical disagreements to the world of search and recommendation systems is a disagreement for another time.
What I’m excited about is that the intersection of microeconomics and information retrieval opens up a huge area of cross-fertilization. For example, one thing I’m fascinated about is the idea that maybe we can use this system to maximize ANY utility metric. Indeed, the authors of LambdaMART point out this possibility. The lambda insight can be used with really any utility metric that can compute differences between preference lists. Could our grades be replaced with a direct measure of monetary value? Is there a way to compute utility for a user using econometrics measures that are actually better than relevance measures like NDCG and ERR? I actually don’t know, but it’s an area I’m excited to explore. Luckily OSC founder Eric Pugh has a degree in economics…
The industry’s untackled challenge: two-way search-driven markets
So far, we’ve discussed one way markets where only the buyer’s utility is maximized. The poorly kept secret in search is that the shopkeeper isn’t quite Santa. Selfless Santa only cares about maximizing joy of the world’s children. The shopkeeper has to maximize his utility (i.e. maximizing profit) and isn’t just interested in selflessly serving the interests of users. Even more complex are search systems that act as market places. Where multiple sellers hawk their wares (be they products, jobs, dates, or whatever) to a diverse group of buyers. Here not only must you satisfy your buyers, but also balance the needs of sellers who might also be the paying customer of your service.
So now I lull myself to sleep thinking about problems with search and recommendations (everything here applies to recasts as well) and two-way marketplaces. I’ve come up with a few ideas
Lambdas per seller
First, a seller’s preference can be described also by a judgment list, ordered by the product they’d like to get in front of a neutral buyer’s eyes. Perhaps ordered by the most profitable. Going back to our fashion search example, our fashion line would rather sell you overpriced Yoga pants than cheap running shorts. This can also be expressed by a judgment list:
#Fitness Seller:
4 qid:999 product1234 # expensive yoga pants
1 qid:999 product4214 # cheap running shortsNow we wouldn’t just layer this directly as another example into our learning to rank solution. As what that would do would maximize the NDCG for “Fitness Seller”. We want to maximize the NDCG for ‘Fitness Seller’ when Bob is searching with a keyword ‘running shorts’.
So one idea I’d have is to modify the psuedoresponse calculations by incorporating BOTH the user’s preference AND every potential seller’s preference. In other words, we change deltaNDCG to incorporate multiple utility measures:
deltaNDCGSeller1 = (oldNDCGSeller1 - newNDCGSeller1)
deltaNDCGSellerN = (oldNDCGSellerN - newNDCGSellerN)
deltaNDCG = (oldNDCG - newNDCG) + (weightSeller1 * deltaNDCGSeller1) + (weightSeller2 * deltaNDCGSeller2) …+ (weightSellerN * deltaNDCGSellerN)(Of course as before, NDCG can be replaced by any other utility metric)
As these pseudo responses are forces tugging the search results up and down we can calibrate the “tug” used during learning to rank. to incorporate both buyer and (perhaps competing) seller needs. This lets us use features of users, keyword queries, products that can predict the balanced utility ordering.
Simple reranking
Another approach could be to simply have competing models. In Elasticsearch and Solr learning to rank, multiple rescoring phases are possible. As it’s unlikely you’d want to completely screw up what will maximize a buyer’s utility, you can instead offer small tie breaks in a rescoring phase that executes a seller-biased model (or set of models). Perhaps it could incorporate all the seller’s lambda’s in the previous section.
These two ideas are my initial forray, but I’m interested in hearing from you on ideas you might have.
Get in touch!
That’s it for now. Do get in touch with us if we can work with you on a challenging search strategy, relevance or learning to rank problem. We’d love to hear from you!